Eine kleine Lernwelt

1. Das Kalorimeter: Ein präzises Messinstrument

In der vorherigen Lektion haben wir grundlegende kalorimetrische Experimente kennengelernt. Dabei haben wir vereinfacht angenommen, dass die gesamte freigesetzte Wärme vom Wasser aufgenommen wird. In präziseren Messungen müssen wir jedoch berücksichtigen, dass auch das Messgerät selbst - das Kalorimeter - einen Teil der Wärmeenergie aufnimmt.

Was ist ein Kalorimeter?

Ein Kalorimeter ist ein spezielles Messgerät zur Bestimmung der bei einer Reaktion aufgenommenen oder abgegebenen Wärmeenergie:

Thermisch isoliertes System (minimaler Wärmeaustausch mit der Umgebung)
Präzise Temperaturmessung
Bekannte Wärmekapazität des gesamten Systems
Eingebautes Rührwerk für gleichmäßige Wärmeverteilung

Typen von Kalorimetern

Es gibt verschiedene Arten von Kalorimetern für unterschiedliche Anwendungen:

Bombenkalorimeter: Für Verbrennungsreaktionen unter hohem Druck
Reaktionskalorimeter: Für flüssige Reaktionssysteme
Differentialkalorimeter (DSC): Für die Messung von Wärmeflüssen
Isothermes Titrationskalorimeter: Für biochemische Prozesse

2. Die Wärmekapazität des Kalorimeters

Die Wärmekapazität eines Kalorimeters gibt an, wie viel Energie nötig ist, um das gesamte Kalorimeter (Gefäß, Thermometer, Rührer etc.) um 1 Kelvin zu erwärmen. Diese Gerätekonstante wird auch als Kalorimeterkonstante oder Wasserwert bezeichnet.

Berücksichtigung der Kalorimeterkonstante in der Wärmeenergie-Berechnung:

Q_ges = (m_Wasser · c_Wasser + C_Kal) · ΔT

wobei:

Q_ges = Gesamte Wärmeenergie in Joule (J)
m_Wasser = Masse des Wassers in Kilogramm (kg)
c_Wasser = spezifische Wärmekapazität von Wasser (4,184 J/(g·K))
C_Kal = Kalorimeterkonstante in J/K
ΔT = Temperaturänderung in Kelvin (K) oder °C

Bestimmung der Kalorimeterkonstante

Um genaue Messungen durchführen zu können, muss zunächst die Kalorimeterkonstante bestimmt werden. Dies geschieht mit Hilfe einer Kalibrierungsmessung, bei der eine bekannte Wärmemenge zugeführt wird.

Methode 1: Elektrische Kalibrierung

Ein elektrischer Widerstand wird im Kalorimeter platziert und eine genau gemessene elektrische Energiemenge zugeführt:

Q_elektrisch = U · I · t (Spannung × Stromstärke × Zeit)

Anschließend wird die Kalorimeterkonstante bestimmt:

C_Kal = (Q_elektrisch / ΔT) - (m_Wasser · c_Wasser)

Methode 2: Chemische Kalibrierung

Eine Reaktion mit bekannter Reaktionsenthalpie (z.B. Neutralisation von Salzsäure mit Natronlauge) wird durchgeführt:

C_Kal = (|ΔH_R| · n) / ΔT - (m_Wasser · c_Wasser)

Dabei ist n die Stoffmenge und ΔH_R die molare Reaktionsenthalpie der Kalibrierungsreaktion.

3. Präzise Messungen mit dem Kalorimeter

Die Verwendung eines Kalorimeters ermöglicht präzise Messungen der Reaktionswärme. Dabei ist es wichtig, verschiedene Faktoren zu berücksichtigen, um die Genauigkeit zu maximieren.

Experimentelles Vorgehen

Kalibrierung des Kalorimeters (Bestimmung der Kalorimeterkonstante)
Exakte Bestimmung der eingesetzten Stoffmengen
Messung der Anfangstemperatur (nach Temperaturausgleich)
Durchführung der Reaktion unter ständigem Rühren
Beobachtung des Temperaturverlaufs bis zum Erreichen des Maximums/Minimums
Berücksichtigung von Wärmeverlusten (ggf. Extrapolation des Temperaturverlaufs)

Wichtig für präzise Messungen:

Für genaue Messergebnisse sollten folgende Faktoren beachtet werden:

Thermische Isolierung des Kalorimeters überprüfen
Rührer kontinuierlich mit konstanter Geschwindigkeit betreiben
Alle Komponenten vor Reaktionsbeginn auf gleiche Temperatur bringen
Temperaturmessfühler kalibrieren
Bei längeren Messungen Wärmeverluste durch mathematische Korrektur berücksichtigen

Berechnung der Reaktionsenthalpie unter Berücksichtigung des Kalorimeters:

ΔH_R = -Q_ges / n

ΔH_R = -(m_Wasser · c_Wasser + C_Kal) · ΔT / n

Dabei ist n die umgesetzte Stoffmenge des Reaktanden (in mol).

4. Praktisches Beispiel: Neutralisationsreaktion

Die Neutralisation einer starken Säure mit einer starken Base ist ein klassisches Beispiel für eine exotherme Reaktion, die gut mit einem Kalorimeter gemessen werden kann.

Reaktionsgleichung:

HCl (aq) + NaOH (aq) → NaCl (aq) + H₂O (l) + Wärme

H⁺ (aq) + OH^- (aq) → H₂O (l)

Beispielrechnung mit Kalorimeter:

Angenommen, wir haben folgende Messwerte:

50 mL 1,0 M HCl-Lösung
50 mL 1,0 M NaOH-Lösung
Anfangstemperatur beider Lösungen: 22,0°C
Endtemperatur nach der Reaktion: 28,5°C
Kalorimeterkonstante: C_Kal = 75 J/K

Berechnung:

Gesamtmasse des Wassers: m_Wasser = 100 g (näherungsweise, da verdünnte Lösungen)
Temperaturänderung: ΔT = 28,5°C - 22,0°C = 6,5 K
Umgesetzte Stoffmenge: n = 0,05 L · 1,0 mol/L = 0,05 mol
Gesamte Wärmeenergie:
Q_ges = (m_Wasser · c_Wasser + C_Kal) · ΔT
Q_ges = (100 g · 4,184 J/(g·K) + 75 J/K) · 6,5 K
Q_ges = (418,4 J/K + 75 J/K) · 6,5 K
Q_ges = 493,4 J/K · 6,5 K = 3207,1 J
Molare Reaktionsenthalpie:
ΔH_R = -Q_ges / n
ΔH_R = -3207,1 J / 0,05 mol
ΔH_R = -64142 J/mol = -64,1 kJ/mol

Der Literaturwert für die Neutralisationsenthalpie beträgt etwa -57,3 kJ/mol. Die Abweichung kann durch Wärmeverluste und Messungenauigkeiten erklärt werden.

5. Eigene Berechnung

Berechne selbst die Reaktionsenthalpie für verschiedene Messwerte unter Berücksichtigung der Kalorimeterkonstante:

Volumen der Lösungen (mL):
Konzentration der Lösungen (mol/L):
Anfangstemperatur (°C):
Endtemperatur (°C):
Kalorimeterkonstante (J/K):

6. Fortgeschrittene Kalorimetrie: Wärmeverlustkorrektur

Bei längeren Messungen kann der Wärmeverlust an die Umgebung nicht vernachlässigt werden. In professionellen Messungen wird dieser Faktor durch mathematische Verfahren korrigiert.

Korrekturmethoden

Regnault-Pfaundler-Methode

Eine klassische Methode zur Korrektur von Wärmeverlusten durch Extrapolation der Temperaturkurven vor und nach der Reaktion.

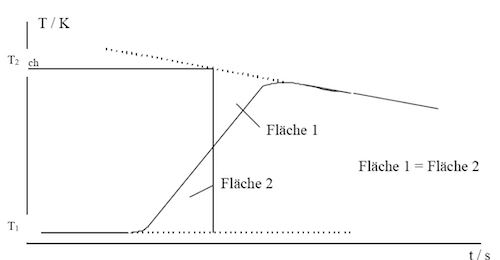
Dickinson-Methode

Bestimmung des Temperaturmaximums/-minimums durch graphische Extrapolation der Temperaturkurve.

Die moderne Kalorimetrie nutzt computergestützte Auswerteverfahren, um Wärmeverluste zu korrigieren und die Genauigkeit der Messungen weiter zu erhöhen. Dabei werden Differentialgleichungen gelöst, um den Wärmefluss zwischen Kalorimeter und Umgebung zu modellieren.

7. Anwendungen der präzisen Kalorimetrie

Die exakte Bestimmung von Reaktionswärmen und Wärmekapazitäten ist in vielen Bereichen von Wissenschaft und Technik wichtig.

Wissenschaftliche Anwendungen

Bestimmung thermodynamischer Daten für die chemische Datenbank
Untersuchung von Protein-Ligand-Wechselwirkungen in der Biochemie
Messung von Phasenübergängen in Materialien
Bestimmung von Reinheitsgraden chemischer Substanzen

Technische Anwendungen

Bestimmung des Brennwerts von Kraftstoffen und Nahrungsmitteln
Qualitätskontrolle in der chemischen Industrie
Sicherheitsuntersuchungen für exotherme Reaktionen
Optimierung von Verbrennungsprozessen

Moderne Kalorimeter im Labor

Entdecke die neuesten Entwicklungen in der Kalorimeterforschung und erfahre mehr über hochpräzise Messgeräte.

Zu den Gerätevorstellungen →

8. Übungsaufgaben zur Kalorimetrie

Übungsaufgabe 1: Bestimmung der Kalorimeterkonstante

Ein elektrischer Heizwiderstand wird in ein Kalorimeter mit 250 g Wasser gegeben. Bei einer angelegten Spannung von 12 V und einer Stromstärke von 0,5 A steigt die Temperatur in 5 Minuten von 20,0°C auf 23,5°C. Berechne die Kalorimeterkonstante.

Lösung:

Zugeführte elektrische Energie: Q_el = U · I · t = 12 V · 0,5 A · 300 s = 1800 J

Wärmekapazität des Wassers: C_Wasser = m · c = 250 g · 4,184 J/(g·K) = 1046 J/K

Temperaturänderung: ΔT = 23,5°C - 20,0°C = 3,5 K

C_Kal = (Q_el / ΔT) - C_Wasser = (1800 J / 3,5 K) - 1046 J/K = 514,3 J/K - 1046 J/K = 468,3 J/K

Übungsaufgabe 2: Reaktionsenthalpie einer Verdünnungsreaktion

In einem Kalorimeter mit einer Kalorimeterkonstante von 120 J/K befinden sich 100 g Wasser bei 22,0°C. Nach Zugabe von 5,0 g konzentrierter Schwefelsäure (H₂SO₄) steigt die Temperatur auf 35,2°C. Berechne die molare Verdünnungswärme der Schwefelsäure.